Visualizing Molecular Dipole Moment

Problem

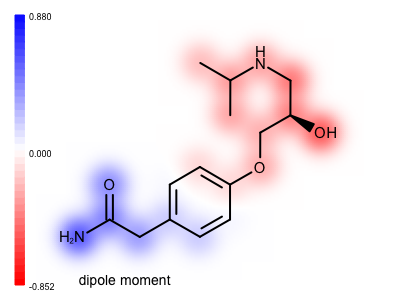
You want to visualize the molecular dipole moment that is a good indicator of the overall polarity of a molecule. See example in Figure 1.

Figure 1. Example of visualizing the molecular dipole moment

Ingredients

Difficulty level

../_images/chilly7.png ../_images/chilly7.png ../_images/chilly7.png

Download

Download code

dipole2img.py

See also the Usage subsection.

Solution

The calculate_dipole_moment function, after assigning the partial charges of the atoms by calling the OEMMFF94PartialCharges function, calculates the center of the positive and negative charges (lines 16-28) using the partial atom charges as a weight. Then its calculates:

  • the magnitude of the dipole (lines 36-44)
  • the (unit normalized) direction of the dipole (lines 46-48)
  • the center of the dipole (lines 50-52)

The dipole inner product is then calculated for each atom.. This is the vector product of the unit dipole with the vector from the dipole center to the atom center (lines 56-58). These numbers are then normalized such that the most positive number is equal to 1.0 and the most negative to -1.0 (lines 54-59). After the normalization, the number are attached to the relevant atom as generic data with the given tag (lines 66-67). For each bond a value is also calculated by averaging the values of its end atoms See more details in the Discussion section.

Note

The dipole inner product numbers represent both the distance and correlation with direction of the dipole, i.e. an atom that is in the positive direction of the dipole will be positive and its value will be bigger the further away it is from the center of the dipole. Atoms that are in a plane orthogonal to the dipole, passing through the dipole center, will have a number close to zero.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
def calculate_dipole_moment(mol, itag):
    """
    Calculates dipole moment for each atom.

    :type mol: oechem.OEMolBase
    :type: itag: int
    """

    oechem.OEMMFFAtomTypes(mol)
    oechem.OEMMFF94PartialCharges(mol)

    ncrg = 0.0
    pcrg = 0.0
    ncen = [0.0, 0.0, 0.0]
    pcen = [0.0, 0.0, 0.0]
    for atom in mol.GetAtoms():
        charge = atom.GetPartialCharge()
        x, y, z = mol.GetCoords(atom)
        if charge < 0.0:
            ncen[0] -= charge * x
            ncen[1] -= charge * y
            ncen[2] -= charge * z
            ncrg -= charge
        elif charge > 0.0:
            pcen[0] += charge * x
            pcen[1] += charge * y
            pcen[2] += charge * z
            pcrg += charge

    for idx in range(0, 3):
        ncen[idx] = ncen[idx] / ncrg
        pcen[idx] = pcen[idx] / pcrg
    if pcrg > ncrg:
        pcrg = ncrg

    dpmag = 0.0
    for i in range(0, 3):
        dpmag += (ncen[i] - pcen[i]) * (ncen[i] - pcen[i])

    if abs(dpmag) < 0.001:
        # no dipole moment
        return False

    dpmag *= 4.80324 * pcrg

    dipdir = [0.0, 0.0, 0.0]
    for idx in range(0, 3):
        dipdir[idx] = 4.80324 * pcrg * ((pcen[idx] - ncen[idx]) / dpmag)

    dipcen = [0.0, 0.0, 0.0]
    for idx in range(0, 3):
        dipcen[idx] = 0.5 * (pcen[idx] + ncen[idx])

    dpip = oechem.OEFloatArray(mol.GetMaxAtomIdx())

    for atom in mol.GetAtoms():
        x, y, z = mol.GetCoords(atom)
        dpip[atom.GetIdx()] = sum([(x - dipcen[0]) * dipdir[0],
                                   (y - dipcen[1]) * dipdir[1],
                                   (z - dipcen[2]) * dipdir[2]])

    max_dpip = max(dpip)
    min_dpip = min(dpip)

    dpip = [-i / min_dpip if i < 0.0 else i for i in dpip]
    dpip = [+i / max_dpip if i > 0.0 else i for i in dpip]

    for atom, dipole in zip(mol.GetAtoms(), dpip):
        atom.SetData(itag, dipole)

    for bond in mol.GetBonds():
        avg = (bond.GetBgn().GetData(itag) + bond.GetEnd().GetData(itag)) / 2.0
        bond.SetData(itag, avg)

    return True

The depict_molecule_with_dipole function below shows how the atom values calculated by the calculate_dipole_moment function are projected onto the property map. This gives you a sense of the direction of the dipole relative to the atoms. Before rendering the molecule the OEPrepareDepictionFrom3D function is called to generate a 2D layout of the molecule that is most similar to the 3D coordinates (line 3). The atom values are then projected onto the 2D diagram using the OE2DPropMap class (lines 10-12).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
def depict_molecule_with_dipole(image, mol, opts, stag):
    """
    Depicts the molecule property map.

    :type image: oedepict.OEImageBase
    :type mol: oechem.OEMolBase
    :type opts: oedepict.OE2DMolDisplayOptions
    :type stag: string
    """

    oegrapheme.OEPrepareDepictionFrom3D(mol, True)

    opts.SetAtomColorStyle(oedepict.OEAtomColorStyle_WhiteMonochrome)
    opts.SetScale(oegrapheme.OEGetMoleculeSurfaceScale(mol, opts))

    disp = oedepict.OE2DMolDisplay(mol, opts)

    propmap = oegrapheme.OE2DPropMap(opts.GetBackgroundColor())
    propmap.SetLegendLocation(oegrapheme.OELegendLocation_Left)
    propmap.Render(disp, stag)

    oedepict.OERenderMolecule(image, disp)

Usage

Usage

dipole2img.py and atenolol.sdf molecule file

The following command will generate the image shown in Figure 1.

prompt > python3 dipole2img.py atenolol.sdf atenolol.svg

Command Line Parameters

Simple parameter list
    -height : Height of output image
    -width : Width of output image

    input/output options
      -in : Input molecule filename
      -out : Output filename of the generated image

Discussion

In the calculate_dipole_moment function, after calculating the atom values, a value is calculated for each bond by averaging the values of its end atoms (lines 58-60). When the property map is rendered these bond values are projected at the middle of the bond resulting in a much smoother image. See the difference between the two images shown below. Image (A) is generated by projecting only atom values, while in image (B) both the atom and the bond values are projected onto the property map before applying a Gaussian function to blur out the 2D grid underneath the molecular graph.

Table 1.
( A ) only atom values ( B ) both atom and bond values
../_images/dipole2img-nobond.png

See also in OEChem TK manual

Theory

API

See also in OEDepict TK manual

Theory

API

See also in GraphemeTM TK manual

Theory

API