Drawing ROC Curve

Problem

You want to draw a ROC curve to visualize the performance of a binary classification method (see Figure 1).

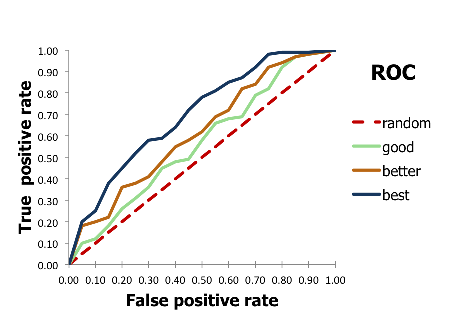
Figure 1. Example of ROC curves

Ingredients

matplotlib - Python 2D Plotting Library scikit-learn - Machine Learning in Python

Difficulty level

Download

Download code

roc2img.py

See also the Usage subsection.

Solution

Binary classification is the task of classifying the members of a given set of objects into two groups on the basis of whether they have some property or not. There are four possible outcomes from a binary classifier (see Figure 2):

• true positive (TP) : predicted to be positive and the actual value is also positive
• false positive (FP) : predicted to be positive but the actual value is negative
• true negative (TN) : predicted to be negative and the actual value is also negative
• false negative (FN) : predicted to be negative but the actual value is positive

In molecule modeling, the positive entities are commonly called actives, while the negative ones are called decoys.

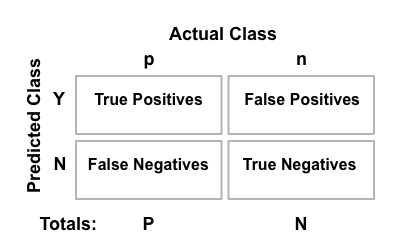
Figure 2. The confusion matrix

From the above numbers the followings can be calculated:

• true positive rate: \(TPR = \frac{positives\ correctly \ classified}{total\ positives} = \frac{TP}{P}\)
• false positive rate: \(FPR = \frac{negatives\ incorrectly\ classified}{total\ negatives} = \frac{FP}{N}\)

The receiver operating characteristic (ROC) curve is a two dimensional graph in which the false positive rate is plotted on the X axis and the true positive rate is plotted on the Y axis. The ROC curves are useful to visualize and compare the performance of classifier methods (see Figure 1).

Figure 3 illustrates the ROC curve of an example test set of 18 entities (7 actives, 11 decoys) that are shown in Table 1 in the ascending order of their scores. For a small test set, the ROC curve is actually a stepping function: an active entity in Table 1 moves the line upward, while a decoy moves it to the right.

Table 1. Example data for ROC

id	score	active/decoy	id	score	active/decoy
O	0.03	a	L	0.48	a
J	0.08	a	K	0.56	d
D	0.10	d	P	0.65	d
A	0.11	a	Q	0.71	d
I	0.22	d	C	0.72	d
G	0.32	a	N	0.73	a
B	0.35	a	H	0.80	d
M	0.42	d	R	0.82	d
F	0.44	d	E	0.99	d

Figure 3. Example of ROC curve

The following code snippet shows how to calculate the true positive and false positive rates for the plot shown in Figure 3. The get_rates function that takes the following parameters:

actives

A list of id of actives. In our simple example of Table 1 the actives are: [‘A’, ‘B’, ‘G’, ‘J’, ‘L’, ‘N’, ‘O’]

scores

A list of (id, score) tuples in ascending order of the scores.

It generates the tpt and fpt values i.e. the increasing true positive rates and positive rates, respectively. Alternatively, the tpt and fpt values can be calculated using the sklearn.metrics.roc_curve() function. See example in Plotting ROC Curves of Fingerprint Similarity.

Note

In this simple example the scores are in the range of [0.0, 1.0], where the lower the score is the better. For different score range the functions have to be modified accordingly.

def get_rates(actives, scores):
    """
    :type actives: list[sting]
    :type scores: list[tuple(string, float)]
    :rtype: tuple(list[float], list[float])
    """

    tpr = [0.0]  # true positive rate
    fpr = [0.0]  # false positive rate
    nractives = len(actives)
    nrdecoys = len(scores) - len(actives)

    foundactives = 0.0
    founddecoys = 0.0
    for idx, (id, score) in enumerate(scores):
        if id in actives:
            foundactives += 1.0
        else:
            founddecoys += 1.0

        tpr.append(foundactives / float(nractives))
        fpr.append(founddecoys / float(nrdecoys))

    return tpr, fpr

The following code snippets show how the image of the ROC curve (Figure 3) is generated from the true positive and false positive rates calculated by the get_rates function.

def depict_ROC_curve(actives, scores, label, color, filename, randomline=True):
    """
    :type actives: list[sting]
    :type scores: list[tuple(string, float)]
    :type color: string (hex color code)
    :type fname: string
    :type randomline: boolean
    """

    plt.figure(figsize=(4, 4), dpi=80)

    setup_ROC_curve_plot(plt)
    add_ROC_curve(plt, actives, scores, color, label)
    save_ROC_curve_plot(plt, filename, randomline)

def setup_ROC_curve_plot(plt):
    """
    :type plt: matplotlib.pyplot
    """

    plt.xlabel("FPR", fontsize=14)
    plt.ylabel("TPR", fontsize=14)
    plt.title("ROC Curve", fontsize=14)

The AUC number of the ROC curve is also calculated (using sklearn.metrics.auc()) and shown in the legend. The area under the curve (AUC) of ROC curve is an aggregate measure of performance across all possible classification thresholds. It ranges between \([0.0, 1.0]\). The model with perfect predictions has an AUC of 1.0 while a model that always gets the predictions wrong has a AUC value of 0.0.

def add_ROC_curve(plt, actives, scores, color, label):
    """
    :type plt: matplotlib.pyplot
    :type actives: list[sting]
    :type scores: list[tuple(string, float)]
    :type color: string (hex color code)
    :type label: string
    """

    tpr, fpr = get_rates(actives, scores)
    roc_auc = auc(fpr, tpr)

    roc_label = '{} (AUC={:.3f})'.format(label, roc_auc)
    plt.plot(fpr, tpr, color=color, linewidth=2, label=roc_label)

def save_ROC_curve_plot(plt, filename, randomline=True):
    """
    :type plt: matplotlib.pyplot
    :type fname: string
    :type randomline: boolean
    """

    if randomline:
        x = [0.0, 1.0]
        plt.plot(x, x, linestyle='dashed', color='red', linewidth=2, label='random')

    plt.xlim(0.0, 1.0)
    plt.ylim(0.0, 1.0)
    plt.legend(fontsize=10, loc='best')
    plt.tight_layout()
    plt.savefig(filename)

Usage

Download code

roc2img.py and supporting data set: actives.txt and scores.txt

The following command will generate the image shown in Figure 3.

prompt > python3 roc2img.py actives.txt scores.txt roc.svg

Discussion

Depicting ROC curves is a good way to visualize and compare the performance of various fingerprint types. The molecule depicted on the left in Table 2 is a random molecule selected from the TXA2 set (49 structures) of the Briem-Lessel dataset. The graph on the right is generated by performing 2D molecule similarity searches using four of the fingerprint types of GraphSim TK (path, circular, tree and MACCS key). The decoy set is the four other activity classes in the dataset (5HT3, ACE, PAF and HMG-CoA) along with an inactive set of randomly selected compounds from the MDDR not known to be belong to any of the five activity classes.

Table 2: Example of ROC curves of fingerprint searches with various types

query	ROC curves

Related Python Cookbook Recipes

• Drawing Fingerprint Score Histogram
• Plotting ROC Curves of Fingerprint Similarity

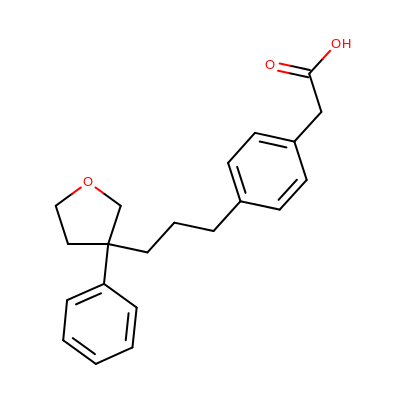
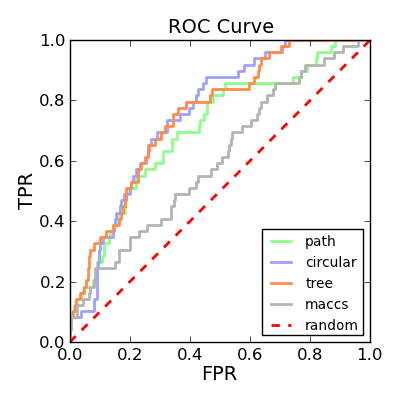
See also in matplotlib documentation

• matplotlib.pyplot

See also in sklearn documentation

• sklearn.metrics.auc()

See also

Theory

• Binary classification in Wikipedia
• Confusion matrix in Wikipedia
• Receiver operating characteristic (ROC) in Wikipedia
• An introduction to ROC analysis by Tom Fawcett
• Area under the curve in Wikipedia

Briem-Lessel Dataset

• [Briem-Lessel-2000]
• MDDR ID’s of the Briem-Lessel Dataset