Finding Core Fragment of a Molecule Series

Problem

You want to find the core fragment in a molecule series i.e. find the largest common substructure of the molecules in a series. See example in Figure 1.

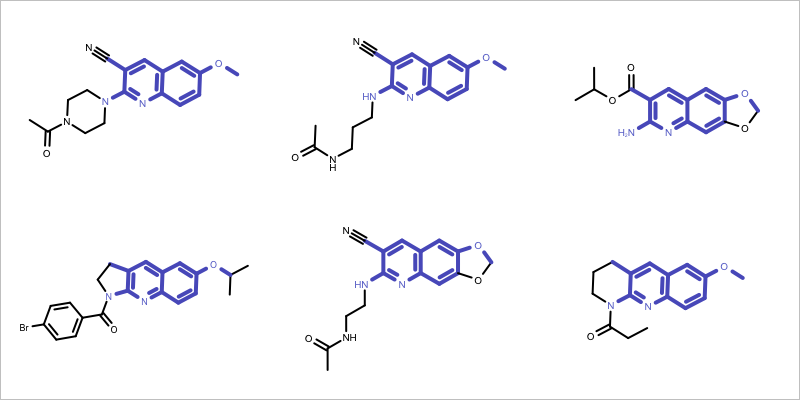
../_images/core-example.png

Figure 1: Example maximum common subgraph of a molecule set

Ingredients

Difficulty Level

../_images/chilly.png ../_images/chilly.png

Solution

The obvious choice to solve this problem is to use a maximum common substructure (MCS) search algorithm.

Definition:

The maximum common subgraph is the largest possible common subgraph of two graphs, i.e. it can not be extended to another common subgraph by the addition of vertices or edges.

The OEChem TK provides the OEMCSSearch class that solves the MCS problem for two molecules. See example in Figure 2.

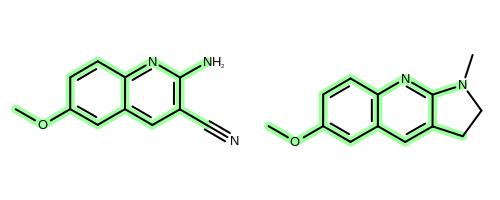
../_images/mcss.png

Figure 2: Example maximum common subgraph of two molecules

MCS is commonly used in cheminformatics to assess molecule similarity. One advantage of MCS over the fingerprinting methods, that it provides an atom - atom mapping between two molecules that is essential to solve this problem.

However, MCS identification belongs to the class of NP-complete problems for which no algorithm with polynomial-time complexity is known for the general case. The identification of all subgraphs containing k nodes that are common to two graphs containing n and m nodes, respectively, requires

\(\frac{m!n!}{(m-k)!(n-k)!k!}\)

atom-by-atom comparisons. The identification of the largest common subgraph is achieved by carrying out this set of comparisons with \(\forall k : 1 < k < min(m, n)\) until it is not possible to identify a larger common substructure. Even though chemical structures do not have high connectivity, which would lead to exponential behavior, it still can be a very expensive operation for large molecules.

The other problem is that the MCS search algorithm implemented in the OEMCSSearch class only works for two molecules. Identifying a MCS for a molecule set would require performing \(n x n\) comparisons. Combining the returned \(n x n\) MCS atom mappings is not a trivial problem either. See example in Figure 3.

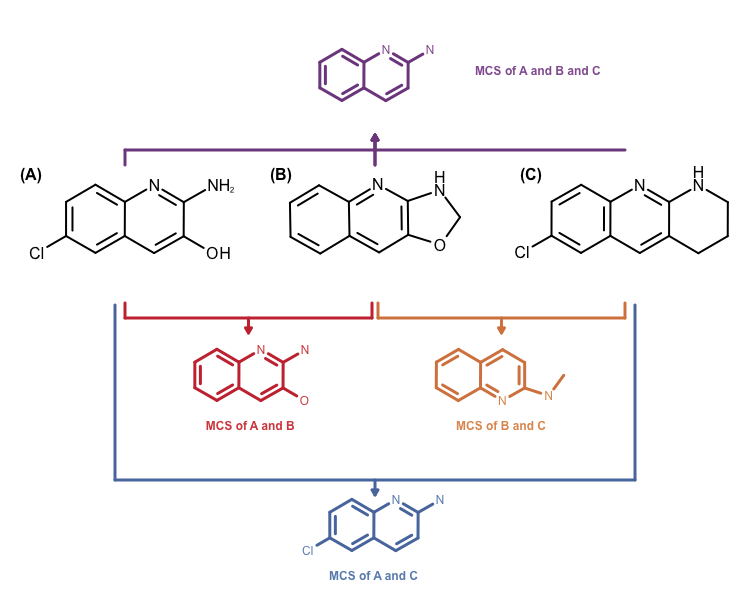
../_images/core-mcss-ABC.png

Figure 3: Example maximum common subgraph of multiple molecules

However the problem we want to solve is quite specific that does not require to perform \(n x n\) MCS searches. If we can assume that a common core does exist in the molecule series than the following process can identify this core fragment:

  • Exhaustively enumerate all fragments in an arbitrary molecule of the series. Choosing a small molecule is preferred since it will have fewer fragments.

  • Perform a substructure search with each fragment to verify whether it is a common fragment, i.e. a substructure of each molecule in the series.

  • Chose the largest common fragment as the core.

The first step of finding a core of a molecule series is to select an arbitrary reference molecule. The GetReferenceMolecule function simply selects the molecule with the smallest number of atoms.

1def GetReferenceMolecule(mollist):
2
3    refmol = None
4    for mol in mollist:
5        if refmol is None or mol.NumAtoms() < refmol.NumAtoms():
6            refmol = mol
7
8    return refmol

The GetFragments function is then called with the reference molecule to enumerate all of its fragments by using functions of GraphSim TK. When generating fingerprints, a molecule graph is exhaustively traversed, enumerating various fragments (using the path, circular or tree method), and then hashing them into a fixed-length bit-vector. The OEGetFPCoverage function of GraphSim TK provides access to these fragments by returning an iterator over OEAtomBondSet objects, each of which stores the atoms and bonds of a specific fragment. See example in Figure 4 that shows how tree fragments are enumerated up to a given length.

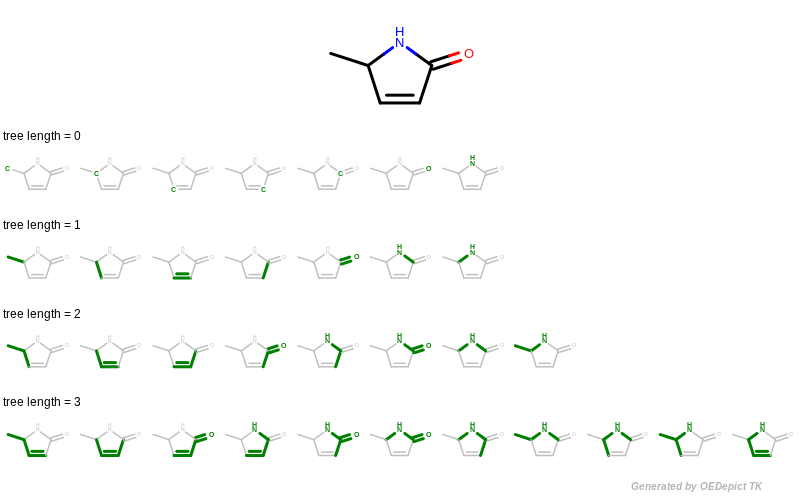
../_images/TreeEnumeration.png

Figure 4: Example of enumerating tree fragments with various lengths

The GetFragments function first generates a tree fingerprint type from a string representation using the OEGetFPType function. Then it loops over the OEAtomBondSet objects returned by the OEGetFPCoverage function and extracts the corresponding molecule fragment using the OESubsetMol function.

 1def GetFragments(mol, minbonds, maxbonds):
 2
 3    frags = []
 4    fptype = oegraphsim.OEGetFPType("Tree,ver=2.0.0,size=4096,bonds=%d-%d,atype=AtmNum,btype=Order"
 5                                    % (minbonds, maxbonds))
 6
 7    for abset in oegraphsim.OEGetFPCoverage(mol, fptype, True):
 8        fragatompred = oechem.OEIsAtomMember(abset.GetAtoms())
 9
10        frag = oechem.OEGraphMol()
11        adjustHCount = True
12        oechem.OESubsetMol(frag, mol, fragatompred, adjustHCount)
13        oechem.OEFindRingAtomsAndBonds(frag)
14        frags.append(oechem.OEGraphMol(frag))
15
16    return frags

Note

When using the OEGetFPCoverage function only fragment size parameter of the fingerprint type is considered. The other parameters such as atom and bond typing are utilized only when hashing the enumerated fragment into a fixed-length bit-vector.

See also

The GetCommonFragments function loops over the fragments enumerated by the GetFragments function and identifies those that are common in the molecule series.

 1def GetCommonFragments(mollist, frags,
 2                       atomexpr=oechem.OEExprOpts_DefaultAtoms,
 3                       bondexpr=oechem.OEExprOpts_DefaultBonds):
 4
 5    corefrags = []
 6
 7    for frag in frags:
 8
 9        ss = oechem.OESubSearch(frag, atomexpr, bondexpr)
10        if not ss.IsValid():
11            continue
12
13        validcore = True
14        for mol in mollist:
15            validcore = ss.SingleMatch(mol)
16            if not validcore:
17                break
18
19        if validcore:
20            corefrags.append(frag)
21
22    return corefrags

The GetCoreFragment is the main function that identifies the common fragments, scores them by calling the GetFragmentScore function and returns one common fragment with the highest score as the core.

 1def GetCoreFragment(mols, minbonds, maxbonds,
 2                    atomexpr=oechem.OEExprOpts_DefaultAtoms,
 3                    bondexpr=oechem.OEExprOpts_DefaultBonds):
 4
 5    print("Number of molecules = %d" % len(mols))
 6
 7    refmol = GetReferenceMolecule(mols)
 8
 9    frags = GetFragments(refmol, minbonds, maxbonds)
10    if len(frags) == 0:
11        oechem.OEThrow.Error("No fragment is enumertated with bonds %d-%d!" % (minbonds, maxbonds))
12
13    print("Number of fragments = %d" % len(frags))
14
15    commonfrags = GetCommonFragments(mols, frags, atomexpr, bondexpr)
16    if len(commonfrags) == 0:
17        oechem.OEThrow.Error("No common fragment is found!")
18
19    print("Number of common fragments = %d" % len(commonfrags))
20
21    core = None
22    for frag in commonfrags:
23        if core is None or GetFragmentScore(core) < GetFragmentScore(frag):
24            core = frag
25
26    return core

GetFragmentScore function gives priority to larger fragments and fragments with more ring atoms.

1def GetFragmentScore(mol):
2
3    score = 0.0
4    score += 2.0 * oechem.OECount(mol, oechem.OEAtomIsInRing())
5    score += 1.0 * oechem.OECount(mol, oechem.OENotAtom(oechem.OEAtomIsInRing()))
6
7    return score

Download code

getcore.py and supporting file getcore.smi

The following example shows the output of the getcore.py script:

Usage:

prompt > python3 getcore.py -in getcore-test.smi

Number of molecules = 459
Number of fragments = 522
Number of common fragments = 372
Core fragment = Cc1cc2cc(ccc2nc1N)O

Discussion

Warning

  • The above algorithm is unable to identify disconnected MCS of multiple molecules, neither does the algorithm that is implemented in the OEMCSSearch class for two molecules. See example in Figure 5.

  • The above algorithm is also not suitable to cluster molecules with more than one core fragments. This is a more complicate problem that can be tackled with performing n x n MCS searches.

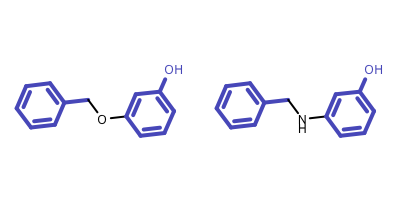
../_images/disconnected-mcs.png

Figure 5: Example of disconnected MCS of two molecules

When performing substructure searches in the GetCommonFragments function the following two options are used: (see Example (A) in Table 1)

  • The OEExprOpts_DefaultAtoms option means that two atoms are considered to be equivalent if they have the same atomic number, aromaticity, and formal charge.

  • The OEExprOpts_DefaultBonds option means that two bonds can be mapped to each other if they have the same bond order and aromaticity.

By modifying the atom and bond expression options, very diverse pattern matching can be performed. Example(B) - Example (D) in Table 1 show examples where the discrimination capability of the OEExprOpts_DefaultAtoms and OEExprOpts_DefaultBonds options are decreased by using various modifiers. This results in identifying larger and larger “common” core fragments. For example, using the OEExprOpts_EqAromatic modifier, atoms in any aromatic ring systems are considered equivalent. As a result, a larger core fragment is identified since the pyridine and pyrimidine rings are considered equivalent.

Table 1. Examples of the effects of using various atom and bond expressions
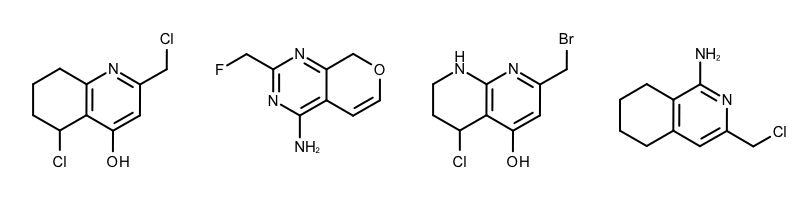
../_images/core-mcss-DefAtoms-DefBonds.png

Example (A) – DefaultAtoms and DefaultBonds
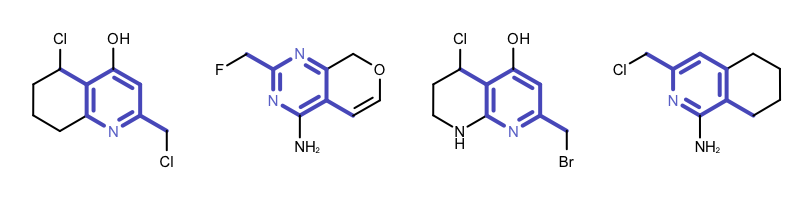
../_images/core-mcss-DefAtomsEqAromatic-DefBonds.png

Example (B) – DefaultAtoms | EqAromatic and DefaultBonds
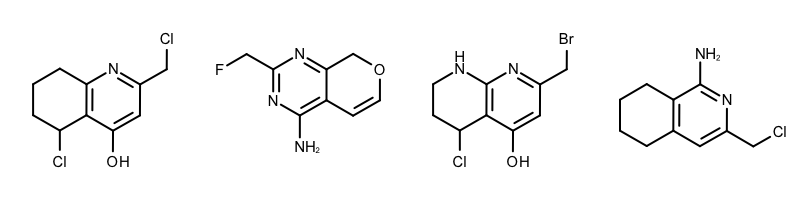
../_images/core-mcss-DefAtomsEqHalogen-DefBonds.png

Example (C) – DefaultAtoms | EqHalogen and DefaultBonds
../_images/core-mcss-DefAtomsEqAromaticEqCAliphaticONS-DefBondsEqSingleDouble.png

Example (D) – DefaultAtoms | EqAromatic | EqCAliphaticONS and DefaultBonds | EqSingleDouble

See also in OEChem TK manual

Theory

API

See also in GraphSim TK manual

API

API

See also

Theory