Similarity Measures¶

The basic idea underlying similarity-based measures is that molecules that are structurally similar are likely to have similar properties. In a fingerprint the presence or absence of a structural fragment is represented by the presence or absence of a set bit. This means that two molecules are judged as being similar if they have a large number of bits in common.

Measuring molecular similarity or dissimilarity has two basic components: the representation of molecular characteristics (such as fingerprints) and the similarity coefficient that is used to quantify the degree of resemblance between two such representations.

Built-in Similarity Measures¶

Since different similarity coefficients quantify different types of structural resemblance, several built-in similarity measures are available in the GraphSim TK (see Table: Basic bit count terms of similarity calculation) The table below defines the four basic bit count terms that are used in fingerprint-based similarity calculations:

**Basic bit count terms of similarity calculation**¶
Symbol	Description
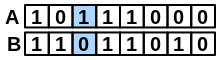
\(onlyA\)	number of bits set “on” in fingerprint A but not in B
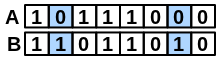
\(onlyB\)	number of bits set “on” in fingerprint B but not in A
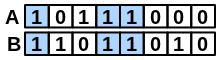
\(bothAB\)	number of bits set “on” in both fingerprints
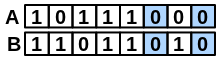
\(neitherAB\)	number of bits set “off” in both fingerprints
\(\|A\|\)	number of bits set “on” in fingerprint A
\(\|B\|\)	number of bits set “on” in fingerprint B
\(fpsize\)	length of fingerprint in bits

Cosine¶

Formula:

\(Sim_{Cosine}(A,B) = \frac{bothAB}{\sqrt{|A|*|B|}} = \frac{bothAB}{\sqrt{(onlyA + bothAB) * (onlyB + bothAB)}}\)

Range:

\([0.0, 1.0]\)

Example:

\(\frac{bothAB}{\sqrt{(onlyA+bothAB)*(onlyB+bothAB)}} = \frac{3}{\sqrt{(1+3)*(2+3)}} = \frac{3}{\sqrt{20}} = 0.67\)

Calculates the ratio of the bits in common to the geometric mean of the number of “on” bits in the two fingerprints.

Dice¶

Formula:

\(Sim_{Dice}(A,B) = \frac{2*bothAB}{|A|+|B|} = \frac{2 *bothAB}{onlyA + onlyB + 2 * bothAB}\)

Range:

\([0.0, 1.0]\)

Example:

\(\frac{2*bothAB}{onlyA+onlyB+2*bothAB}=\frac{2*3}{1+2+2*3}=\frac{6}{9} = 0.666\)

Calculates the ratio of the bits in common to the arithmetic mean of the number of “on” bits in the two fingerprints.

Euclidean¶

Formula:

\(Sim_{Euclid}(A,B) = \sqrt{\frac{bothAB + neitherAB}{fpsize}} = \sqrt{\frac{bothAB + neitherAB}{onlyA + onlyB + bothAB + neitherAB}}\)

Range:

\([0.0, 1.0]\)

Example:

\(\sqrt{\frac{bothAB+neitherAB}{onlyA+onlyB+bothAB+neitherAB}}=\sqrt{\frac{3+2}{1+2+3+2}} = \sqrt{\frac{5}{8}}=0.791\)

Manhattan¶

Formula:

\(Sim_{Manhattan}(A,B) = \frac{onlyA +onlyB}{fpsize} = \frac{onlyA + onlyB}{onlyA + onlyB + bothAB + neitherAB}\)

Range:

\([0.0, 1.0]\)

Example:

\(\frac{onlyA + onlyB}{onlyA + onlyB + bothAB + neitherAB} = \frac{1 + 2}{1 + 2 + 3 + 2} = \frac{3}{8} = 0.375\)

Note

Although \(Sim_{Manhattan}\) shares the same range with other similarity measures, it acts more like a distance measure, scoring more similar fingerprints lower. Identical fingerprints have \(Sim_{Manhattan}\) of 0.0 (as opposed to 1.0 in any other measure).

Tanimoto¶

Formula:

\(Sim_{Tanimoto}(A,B) = \frac{bothAB}{|A| + |B| - bothAB} = \frac{bothAB}{onlyA + onlyB + bothAB}\)

Range:

\([0.0, 1.0]\)

Example:

\(\frac{bothAB}{onlyA+onlyB+bothAB}=\frac{3}{1+2+3}=\frac{3}{6} = 0.5\)

Note

The calculation of the OEFPType::Lingo fingerprint is based on fragmenting canonical isomeric SMILES into overlapping four character long substrings. If any of the two SMILES being compared is shorter than four characters, then their Tanimoto score will be:

1.0, if the two SMILES are identical
0.0, otherwise.

Tversky¶

Formula:

\(Sim_{Tversky}(A,B) = \frac{bothAB}{\alpha * onlyA + \beta * onlyB + bothAB}\)

The Tversky similarity measure is asymmetric. Setting the parameters \(\alpha = \beta = 1.0\) is identical to using the Tanimoto measure.

The factor \(\alpha\) weights the contribution of the first ‘reference’ molecule. The larger \(\alpha\) becomes, the more weight is put on the bit setting of the reference molecule.

Range:

\([0.0, 1.0]\)

Example:

\(\frac{bothAB}{\alpha*onlyA+\beta*onlyB+bothAB} (\alpha=2.0,\beta=1.0)=\frac{3}{2.0*1+1.0*2+3}=\frac{3}{7} = 0.429\)

Note

Although \(Sim_{Tversky}\) shares the same range with other similarity measures, its scaling can vary by orders of magnitude depending on the choice of \(\alpha\) and \(\beta\) parameters.

Similarity Calculation¶

The following example demonstrates how to calculate Tanimoto similarity scores for the molecules depicted in Figure: Example molecules.

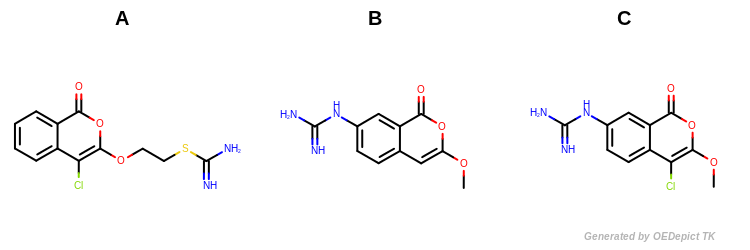
../_images/FingerPrintTanimotoMolecules.png

Example molecules¶

Listing 8: Calculating Tanimoto index

int main( )
{
  OEGraphMol molA;
  OESmilesToMol(molA, "c1ccc2c(c1)c(c(oc2=O)OCCSC(=N)N)Cl");
  OEFingerPrint fpA;
  OEMakeFP(fpA, molA, OEFPType::MACCS166);

  OEGraphMol molB;
  OESmilesToMol(molB, "COc1cc2ccc(cc2c(=O)o1)NC(=N)N");
  OEFingerPrint fpB;
  OEMakeFP(fpB, molB, OEFPType::MACCS166);

  OEGraphMol molC;
  OESmilesToMol(molC, "COc1c(c2ccc(cc2c(=O)o1)NC(=N)N)Cl");
  OEFingerPrint fpC;
  OEMakeFP(fpC, molC, OEFPType::MACCS166);

  std::cout.precision(3);
  std::cout << "Tanimoto(A,B) = " << OETanimoto(fpA, fpB) << std::endl;
  std::cout << "Tanimoto(A,C) = " << OETanimoto(fpA, fpC) << std::endl;
  std::cout << "Tanimoto(B,C) = " << OETanimoto(fpB, fpC) << std::endl;
  return 0;
}

Molecules B and C (shown in Figure: Example Molecules) have the largest Tanimoto value since they share the largest number of common structural features.

For these example molecule the output of Listing 8 is the following:

Tanimoto(A,B) = 0.618
Tanimoto(A,C) = 0.709
Tanimoto(B,C) = 0.889

User-defined Similarity Measures¶

The following code snippet demonstrates how implement the Yule similarity measure with the following formula:

\(Sim_{Yule}(A,B) = \sqrt{\frac{(bothAB * neitherAB) - (onlyA * onlyB)}{(bothAB * neitherAB) + (onlyA * onlyB)}}\)

float CalculateYule(const OEFingerPrint& fpA, const OEFingerPrint& fpB)
{
  unsigned int onlyA, onlyB, bothAB, neitherAB;
  OEGetBitCounts(fpA, fpB, &onlyA, &onlyB, &bothAB, &neitherAB);
  float yule  = (float)(bothAB * neitherAB - onlyA * onlyB);
  yule /= (float)(bothAB * neitherAB + onlyA * onlyB);
  return yule;
}

The OEGetBitCounts function returns the four basic values (namely \(onlyA\), \(onlyB\), \(bothAB\) and \(neitherAB\)) from which any similarity measures can be calculated. For the definition of these values see Table: Basic bit count terms

OEMakeFP(fpA, molA, OEFPType::Path);
OEMakeFP(fpB, molB, OEFPType::Path);
OEMakeFP(fpC, molC, OEFPType::Path);

std::cout << "Yule(A,B) = " << CalculateYule(fpA, fpB) << std::endl;
std::cout << "Yule(A,C) = " << CalculateYule(fpA, fpC) << std::endl;
std::cout << "Yule(B,C) = " << CalculateYule(fpB, fpC) << std::endl;

Warning

User-defined similarity measures can only be used with circular, path, tree, and MACCS key fingerprints but not with LINGO (OEFPType::Lingo).