Ring Perception

Cycle Membership

The simplest form of ring processing in OEChem TK is testing whether an atom or bond is in a ring or not. The OEChem TK function OEFindRingAtomsAndBonds is used to determine which atoms and bonds are members of one or more rings and which are acyclic. This function uses an efficient \(O(n)\) algorithm. Once OEFindRingAtomsAndBonds has been called, an atom or bond can be tested for being in a ring by calling the OEAtomBase.IsInRing or the OEBondBase.IsInRing methods respectively.

The function OEFindRingAtomsAndBonds is called automatically by the high-level file read function OEReadMolecule and OESmilesToMol. However, whenever you modify a molecule by adding or deleting bonds, you’ll need to explicitly call OEFindRingAtomsAndBonds.

The following two ‘equivalent’ code snippets demonstrate how to loop over chain atoms using the OEAtomIsInRing functor and the IsInRing method of the OEAtomBase class.

for atom in mol.GetAtoms(oechem.OENotAtom(oechem.OEAtomIsInRing())):
    print(atom.GetIdx(), oechem.OEGetAtomicSymbol(atom.GetAtomicNum()))

for atom in mol.GetAtoms():
    if not atom.IsInRing():
        print(atom.GetIdx(), oechem.OEGetAtomicSymbol(atom.GetAtomicNum()))

The chain/ring bonds of a molecule can similarly be accessed using the OEBondIsInRing functor and the IsInRing method of the OEBondBase class. For more information about functors see chapter Predicate Functors.

The user can also set the atom and bond ring flags manually using the OEAtomBase.SetInRing and OEBondBase.SetInRing methods.

Code Example

Membership in a Given Ring Size

It is also possible to use OEChem TK to determine whether an atom or a bond is in a ring of a given size, using the OEAtomIsInRingSize and OEBondIsInRingSize functions.

Both of these functions require that OEFindRingAtomsAndBonds has previously been called on the molecule. Both of these functions take the query ring size as an argument, which should be greater than or equal to three. The definition of ring or cycle is not based upon the ‘’smallest set of smallest rings’’ (SSSR), and the functions return true if there is a bonded path of size unique atoms where each atom is bonded to the next and the last is bonded to the first.

It is often the case that atoms may be in different sized cycles at the same time. For example, one way to identify the ring fusion atoms in indole (the fusion of a five-membered pyrrole ring and a six-membered benzene ring) is the following:

for atom in mol.GetAtoms():
    if oechem.OEAtomIsInRingSize(atom, 5) and oechem.OEAtomIsInRingSize(atom, 6):
        print(atom.GetIdx())
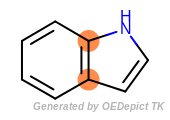
../_images/OEAtomIsInRingSize.png

The fused atoms in indole belong to both a five- and a six-membered rings

OEChem TK also provides an additional pair of functions, OEAtomIsInAromaticRingSize and OEBondIsInAromaticRingSize, to determine whether an atom or bond is in an aromatic ring or cycle of a given size. These behave identically to OEAtomIsInRingSize and OEBondIsInRingSize except that each ring bond in the path/cycle must be aromatic. In addition to OEFindRingAtomsAndBonds, these functions also require the user to have called OEAssignAromaticFlags.

Code Example

Smallest Ring Membership

In addition to determining whether an atom or a bond is in a ring or cycle of a given size, it’s often useful to know the size of the smallest ring or cycle that an atom or bond is in. To do this OEChem TK provides the functions OEAtomGetSmallestRingSize and OEBondGetSmallestRingSize. For acyclic atoms and bonds, these functions return the value zero. For cyclic atoms and bonds, they return a value greater than or equal to three.

for atom in mol.GetAtoms():
    size = oechem.OEAtomGetSmallestRingSize(atom)
    if size == 0:
        print(atom.GetIdx(), "acyclic")
    else:
        print(atom.GetIdx(), "smallest ring size=", size)
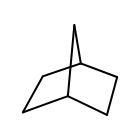
../_images/OEAtomGetSmallestRingSize.png

OEAtomGetSmallestRingSize returns five for each heavy atom of norbornane

Code Example

Connected Components Identification

To aid in splitting molecules into discrete connected components, for example to separate a parent compound from its salt, or a ligand from a protein, OEChem TK provides the function OEDetermineComponents. This function arbitrarily assigns an integer index, starting from one, to each disconnected part in the OEMolBase.

On return this provides a mapping from each atom’s index, obtained by OEAtomBase.GetIdx, to its component index. Unused atom indices are mapped to zero. The function itself also returns the total number of components found, i.e. the maximum part index stored in the array. The following snippet provides a short example of how to use this function.

def MoleculeParts(mol):
    count, parts = oechem.OEDetermineComponents(mol)

    print("The molecule has %d components" % count)
    for atom in mol.GetAtoms():
        print("atom %d is in part %d" % (atom.GetIdx(), parts[atom.GetIdx()]))

Code Example

Ring Systems Identification

The OEChem TK function OEDetermineRingSystems and OEDetermineAromaticRingSystems behave very similarly to the OEDetermineComponents. However, these functions return a mapping from atom indices to a ring or aromatic ring system index, respectively (see example in Listing 1). These functions require that OEFindRingAtomsAndBonds has been called previously. The function OEDetermineAromaticRingSystems also requires the aromaticity perception by calling the OEAssignAromaticFlags function. The OESmilesToMol used in the above example automatically calls both the OEFindRingAtomsAndBonds and OEAssignAromaticFlags functions.

When using the OEDetermineRingSystems function, all acyclic atoms are mapped to the value zero. When using the OEDetermineAromaticRingSystems function, all aliphatic atoms are mapped to the value zero.

Listing 1: Aromatic ring system identification

from openeye import oechem

mol = oechem.OEGraphMol()
oechem.OESmilesToMol(mol, "C(O)(=O)c1cccc2c1[nH]c(C3CCCc4c3cccc4)c2")

nraromsystems, parts = oechem.OEDetermineAromaticRingSystems(mol)

print("Aliphatic atoms:", end=" ")
for atom in mol.GetAtoms():
    if parts[atom.GetIdx()] == 0:
        print(atom.GetIdx(), end=" ")
print()

print("Number of aromatic ring systems =", nraromsystems)

for ringidx in range(1, nraromsystems + 1):
    print(ringidx, ". aromatic ring system:", end=" ")
    for atom in mol.GetAtoms():
        if parts[atom.GetIdx()] == ringidx:
            print(atom.GetIdx(), end=" ")
    print()
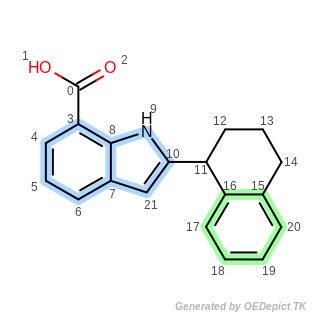
../_images/OEDetermineAromaticRingSystems.png

Example structure of aromatic ring system identification

The output of Listing 1 is the following:

Aliphatic atoms: 0 1 2 11 12 13 14
Number of aromatic ring systems = 2
1 . aromatic ring system: 3 4 5 6 7 8 9 10 21
2 . aromatic ring system: 15 16 17 18 19 20

Code Example

Smallest Set of Smallest Rings (SSSR) Considered Harmful

In graph-theoretical terms, a bond is considered cyclic if its removal from the structure would not lead to the structure being broken into separate components. Despite this simple definition, a large number of algorithms for ring detection exist. (See article [Downs-1989] for an extensive and comparative review.) The diversity and multitude of the ring perception methods derives from the fact that, while determining whether an atom is part of a ring is a very simple problem, the identification of “chemically meaningful” rings among the potentially large number of cyclic subgraphs of a molecular structure can be a surprisingly complex task.

The Smallest set of smallest rings (SSSR) [Plotkin-1971] is the most broadly used type of ring set in computational chemistry. However SSSR is not a unique subset of all possible cycles of a molecule (see Figure: Example of SSSR). Obviously SSSR membership can not be used as a graph theoretical invariant in symmetry perception. Indeed the choice of which rings are part of the SSSR and which are not is arbitrary, and often dependent upon the input order of the molecule. Because of the potential ambiguity of SSSR, many alternative ring set definitions to SSSR have been proposed over the years, including extended SSSR, the set of “synthetically important” rings, the set of elementary rings (SER), the essential set of essential rings (ESER), \(\kappa\)-rings, etc…

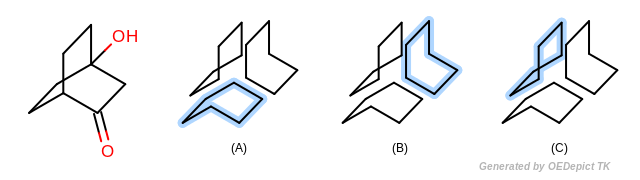
../_images/SSSR.png

Example of SSSR SSSR is not an invariant subset of all possible rings; (a), (b) and (c) depict the three equally valid SSSR of the bridged structure (on the left)

We believe that it is a great service to our customers that we do not include any SSSR functionality in OEChem TK. This is a conscious (and consensus) decision. The forerunners of OEChem TK, Babel and OELib, both contained efficient algorithms for determining SSSR, and these remain freely available on the Internet today. Furthermore, many useful ring perception routines are available in OEChem TK, including:

See also