Surface Generation
Spicoli can generate surfaces from the following other types of objects:
Molecules: Accessible vs Molecular
OESpicoli provides two functions for generating surfaces directly from
molecules: OEMakeAccessibleSurface and
OEMakeMolecularSurface. Both functions require
the definition of a solvent molecule’s probe radius. The default
solvent is water with a probe radius of 1.4 Ångströms .
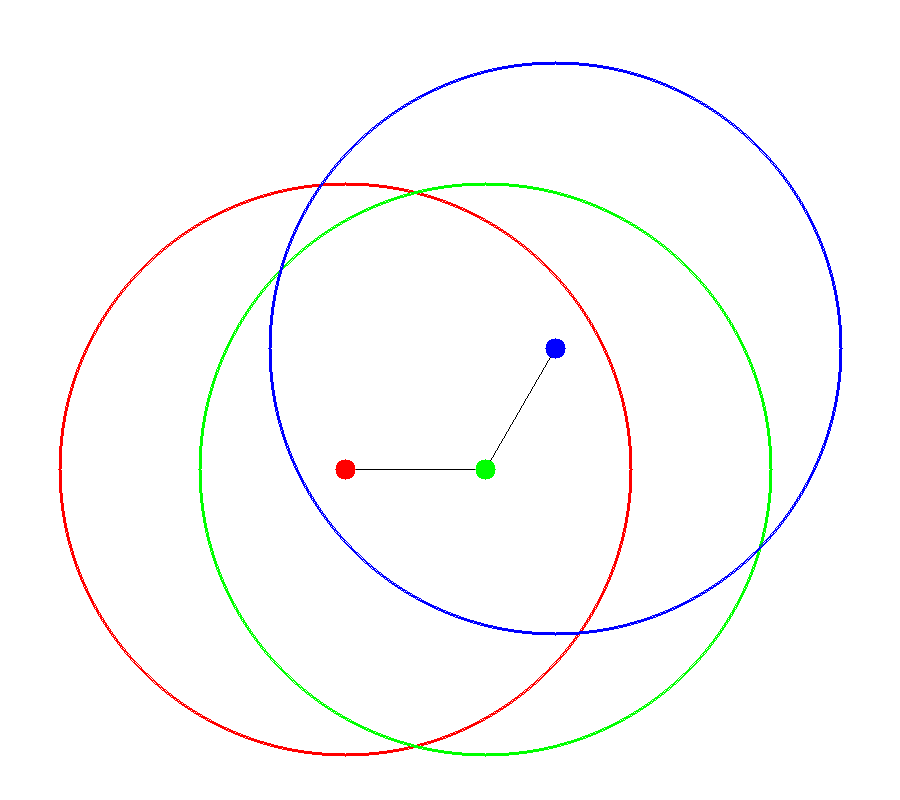
The accessible surface is created by representing each atom as a hard sphere [Lee-1971]. The radius of each sphere is the radius of the atom plus the probe radius. Figures 1 and 2 demonstrate how the spheres are packed together to form the surface. In the figures, portions of the surface are colored based upon each atom’s contribution to the final accessible surface.
|
|
Figure 1 |
Figure 2 |
Accessible Spheres |
Accessible Surface |
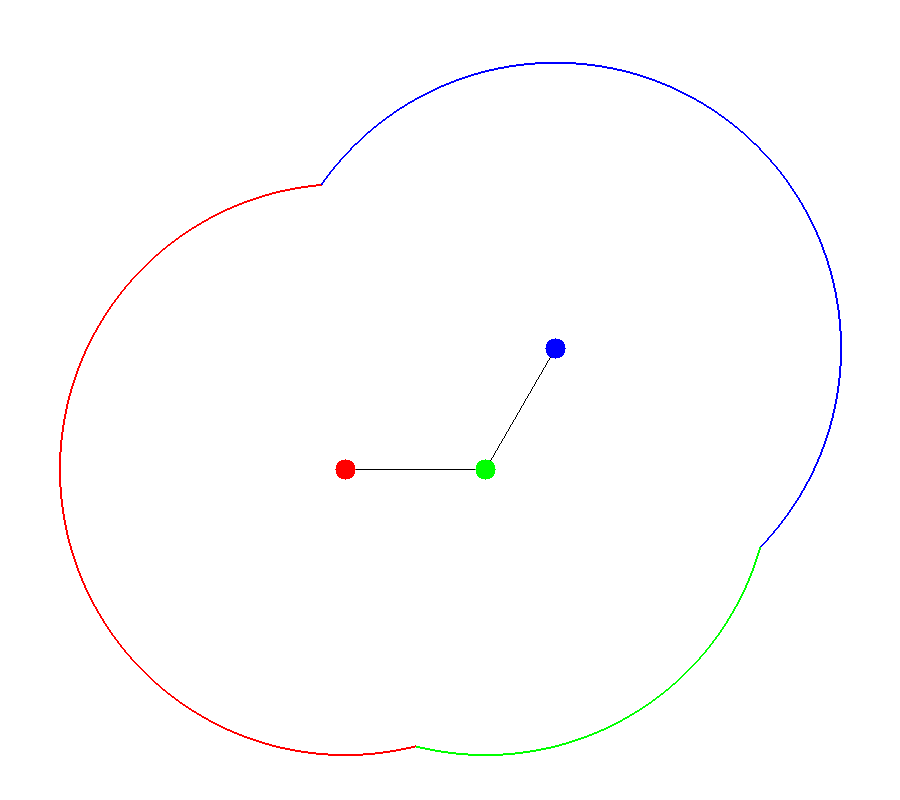
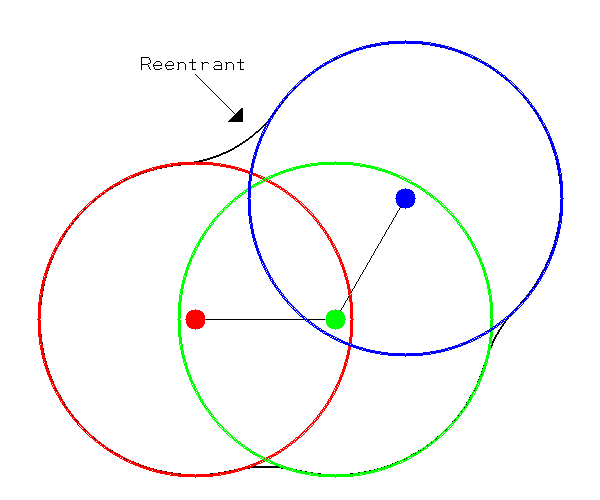
The molecular surface is composed of atom centered spheres plus reentrants [Connolly-1983]. Each sphere’s radius is the atomic radii of the atom it is associated with. The defining characteristic of the molecular surface is the reentrant as shown in Figures 3 and 4. The reentrant models the portion of the molecule inaccessible to solvent. For this reason the volume enclosed by the molecular surface is sometimes referred to as the “solvent-excluded” volume.
|

|
Figure 3 |
Figure 4 |
Molecular Spheres |
Molecular Surface |
Note
The atoms associated with every surface vertex can be obtained by
using the OESurface.GetAtoms
and OESurface.GetAtomsElement methods. For an
accessible surface this is simple to define, it is the atom closest to
the vertex. However, for the molecular surface it is not so clear
because of the re-entrants. Typically, it is the closest atom to
the vertex, but that is not guaranteed. If this guarantee is
required you should call
the OESurfaceToMoleculeDistance function on the
molecule and surface.
Grids
In Spicoli the construction of surfaces from a molecule proceeds through a grid intermediate. The space between grid points determines the resolution of the surface, i.e., how many triangles there are and the size of each triangle. Grids usually consist of equidistant points aligned along orthogonal axes, but this need not always be the case (for instance, electron density grids from crystallography).
Scalar values are placed at every grid point. Surfaces are constructed by tracing out a contour through the grid points. A contour is a separator of points based on whether they are greater than or less than a given value. The separator is a line in two dimensions and a surface in three dimensions. This is similar to how topographic maps use lines to convey elevation.
When dealing with surfaces the points on the grid with a value less
than the chosen contour value are inside the surface and vice versa.
OEMakeSurfaceFromGrid will generate a surface
from a grid using a variation of the marching cubes algorithm.
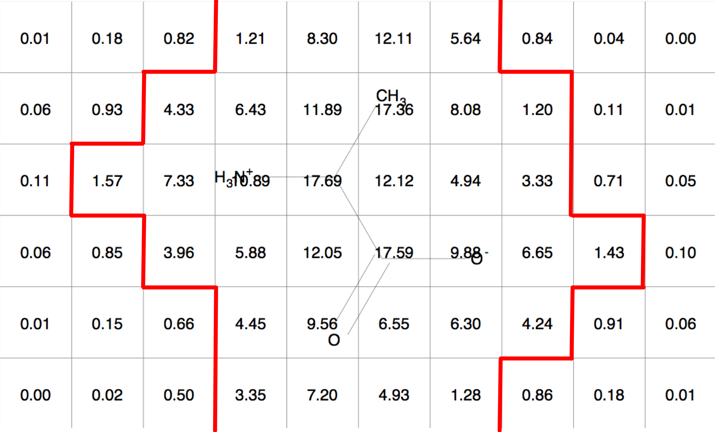
Figure 5 is an example of a two dimensional molecular Gaussian grid for a simple molecule arbitrarily oriented in the grid. Figure 6 shows a contour at 1.0 of that same molecular Gaussian grid.

|
|
Figure 5 |
Figure 6 |
Molecular Gaussian Grid |
Molecular Gaussian Grid Contour |
Hint
Grids and surfaces are fairly interchangeable. A grid can be
constructed from a surface using
the OEMakeGridFromSurface function. Then that
grid can be used to recreate the original surface by using
the OEMakeSurfaceFromGrid function.
Surface Subsets
Surface subsetting is done through the use of Cliques. The triangle, not the vertex, is the most physically relevant intrinsic property of the surface. To maintain a constant surface area for the sum of all partitions Spicoli will not duplicate triangles across surface partitions. However, this does not restrict the duplication of vertices across partitions.
Therefore, the sum of the surface area of every partition will equal
the surface area of the whole surface. The sum
of OESurface.GetNumTriangles over every
partition will equal the total number of triangles in the whole
surface. However, the sum
of OESurface.GetNumVertices over every partition
will not equal the total number of vertices in the whole surface.
See also
Geometric Primitives
Spicoli provides the following free functions to construct surfaces from primitive geometric shapes:
- Boxes:
- Spheres:
- Ellipsoids: