How to Run Benchmark Floes for Cost Estimation
It is a common problem to want to know how much a QM Floe will cost before running it. While there are some back-of-the-envelope calculations we could do, the best approach is to run some very small jobs and then scale the cost of those jobs. The best way to run a small job will vary by the type of floe. Below there are instructions based on the types of floes in the Psi4 QM Package.
In addition, when running low on memory, Psi4 will use more disk space to compensate. This can make calculations slower, and therefore more expensive. So if you plan to change the method or basis set of a calculation away from the default, you may want to investigate how much memory is being used in the calculation (check metrics). Sometimes you may want to repeat the calculation with memory and number of threads increased.
These instructions are to help you understand the CPU time (and money) required to scale up your calculation. By running a job with a single or very few conformers, we can know what it would cost to run the same calculation on hundreds or thousands of molecules or conformers of a similar size. In all cases, we will take the cost of the benchmark job and scale it to estimate the total cost of the larger job.
Orion allows for massively parallel calculations. Therefore, the wall clock time does not scale with the number of calculations being performed. For example, imagine a benchmark calculation where 8 CPUs were used for a geometry optimization on one conformer. If you scaled this job to optimize 1,000 conformers, the cost would be about 1,000 times the benchmark cost. Orion would access enough resources for many copies of the cube to run in parallel, so the wall clock time would not be significantly longer than a single optimization.
Benchmark Torsion Scanning Floes
This process will work for the following floes (with some caveats provided):
Psi4 QM Complete Molecule Torsion Scan In this floe, all rotatable bonds are scanned, so to get the correct approximation you need to multiply the final cost estimated here by the number of rotatable bonds.
Psi4 QM Fragmentation and Torsion Scanning In this floe, the molecule is fragmented around rotatable bonds, so this will be an overestimate. In addition, in step 1 below, you should choose only your smallest molecule since all molecules will be fragmented.
Find or generate a single conformer of the largest molecule you plan to perform a torsion scan on. If your molecules vary significantly in size, you may want to run multiple benchmark jobs with a few different molecules to gauge that effect. This is especially true if you plan to use a larger basis set. If you do not already have 3D coordinates for any of your molecules, then OMEGA - Generate a Single 3D Conformer in Classic Floes can be used to generate one conformer per input molecule.
Locate the appropriate floe for your benchmark calculation. There are two choices for calculations in a torsion scan floe: either a geometry optimization or a single point energy calculation is performed at each angle increment. Choose from these floes:
Psi4 QM Geometry Optimization for torsion scans with geometry optimizations, including any molecules in the Psi4 QM Fragmentation and Torsion Scanning.
Psi4 QM Property Calculation for torsion scans with a single point energy (the Property parameter should be set to Single-Point Energy).
Run your chosen Floe with the single conformer of your molecule, using the method and basis set you plan to use for the torsion scan calculation.
Determine the number of conformers you will have for each torsion scan. The default resolution for a torsion scan is 5 degrees, which leads to 73 conformers. If you plan to change the resolution, the number of conformers is (\(360/resolution + 1\)).
Calculate the total cost, for most floes, as: \($_{benchmark} * N_{conformers} * N_{molecules}\). However, if you are running Psi4 QM Complete Molecule Torsion Scan or Psi4 QM Fragmentation and Torsion Scanning, then you need to account for the number of rotatable bonds in your molecule, so your total cost will be: \($_{benchmark} * N_{conformers} * N_{rotatable\_bonds}\).
Benchmark Conformer Generating Floes
The following floes all generate conformers before performing QM calculations:
In all of these floes, there is a parameter Maximum Conformers for Geometry Optimization. When the number of conformers generated is greater than this number only 1 geometry optimization (and single point energy calculation when relevant) is performed. Run the floe with all other parameters (RMSD, method and basis set, etc.) set as you would for your large scale job, but set the Maximum Conformers for Geometry Optimizations to 1. To calculate the cost of the scaled-up floe, you simply multiply the cost of this job by the number of conformers generated. There are two ways to find the number of conformers.
This information is summarized in the Floe Report for the finished job.
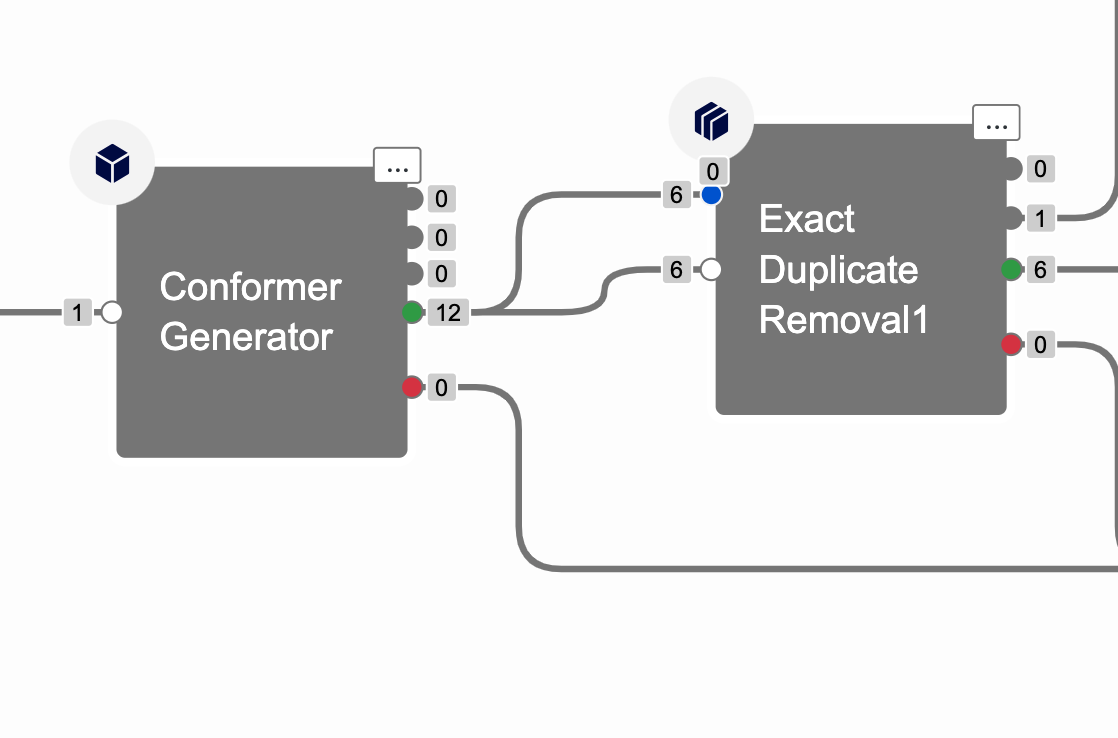
In the job status page, look at the output from the Conformer Generator Cube and divide by 2 for the dual input into the Exact Duplicate Removal Cube. In the example below, there are 6 conformers generated (12 that come out of the Conformer Generator divided by 2).
Benchmark Property Calculation and Geometry Optimization Floes
This process will work for the following two floes:
In the case of simple property calculations and geometry optimizations, there is no exact way of knowing how expensive a single calculation is going to be ahead of time. If you have multiple conformers of the same molecule or a series of molecules fairly similar in size, then you can simply run either of these floes with a single conformer as input and multiply the cost by the number of conformers and molecules you need to run at scale.
If you wish to scale your calculation to larger molecules, the rule of thumb for DFT calculations is that the cost scales as \(N^3\), where \(N\) is the number of atoms in the molecule.
All estimates for cost when scaling up the calculation assume you will use the same method and basis set from the benchmark calculation.