How to Build an Optimal Property-Predicting Machine Learning Model by Tweaking Neural Network Architecture
You can can build multiple learning models based on a set of different cheminformatics and machine learning hyperparameters. The new Keras Hyperparameter Tuner optimizes these hyperparameters to further fine-tune built models.
The model building floe generates several neural network models for every different combination of parameter values supplied. Refer to the tutorial Building Machine Learning Regression Models on how they are built.
If there are n parameters [p1,..pn], with p1 having v1 different values, p2 having v2 different values and so on, there will be [v1*v2*..*vn]*k models built. The k value refers to the additional models the Keras Tuner builds for each hyperparameter combination supplied. This approach employs the commonly used Grid Search Technique [Brownlee-2022] in the neural network community. On top of every course-grained grid search, we further fine-tune the model building process by using tuners as RandomSearch, Hyperband, and Bayesian Optimization. The Floe Report can help to pick the best model to predict properties of previously unseen or new molecules.
To build models, use the ML Build: Regression Model with Tuner using Fingerprints for Small Molecules Floe.
The model learns and predicts exact values. Examples may include:
hERG Toxicity Level in IC50
Permeability Level in IC50 concentration
Solubility Level mol/L
When running this floe, please keep in mind the following information.
To run probability models, turn On the parameter Are We Training Tensorflow Probability.
This option builds TensorFlow probability (TFP) models.
TFP models are better at predicting error bars and domain of application.
Note: this parameter does not use the new Keras Hyperparameter Tuner.
For more information on how to use these models, please refer to the Predict Generic Property of Molecules tutorial.
For each run of the Model Build tool, several fully connected feed-forward neural networks are built (Tutorial FCNN), which predict the physical properties of molecules.
Fully Connected Feed-Forward Neural Network (Fnn)
Dr. Robert Hecht-Nielsen, the inventor of one of the first neurocomputers, defined an Artificial Neural Network as:
… a computing system made up of a number of simple, highly interconnected processing elements, which process information by their dynamic state response to external inputs.
Simply put, a neural network is a set of interconnected nodes or mathematical modules (just like neurons in our brain), which collectively tries to learn a phenomenon (like how permeability is related to a molecule’s composition). It does so by iteratively looking at the training examples (molecular fingerprints in our case) and predicting the property we wish to learn.
In the following explanation, four different optimization strategies are described that will improve the quality of the data and the models.
Optimization Strategy I sets the bit length in accordance to the training size.
Optimization Strategy II selects cheminformatics features based on the nature of the physical property we are trying to predict.
Optimization Strategy III uses hidden nodes, dropouts, and regularizers to prevent underfitting and overfitting of the training data.
Optimization Strategy IV adjusts the regularization parameter or the number of nodes to prevent overfitting.
Architecture
The following figures show the architecture of a neural network and a single node.
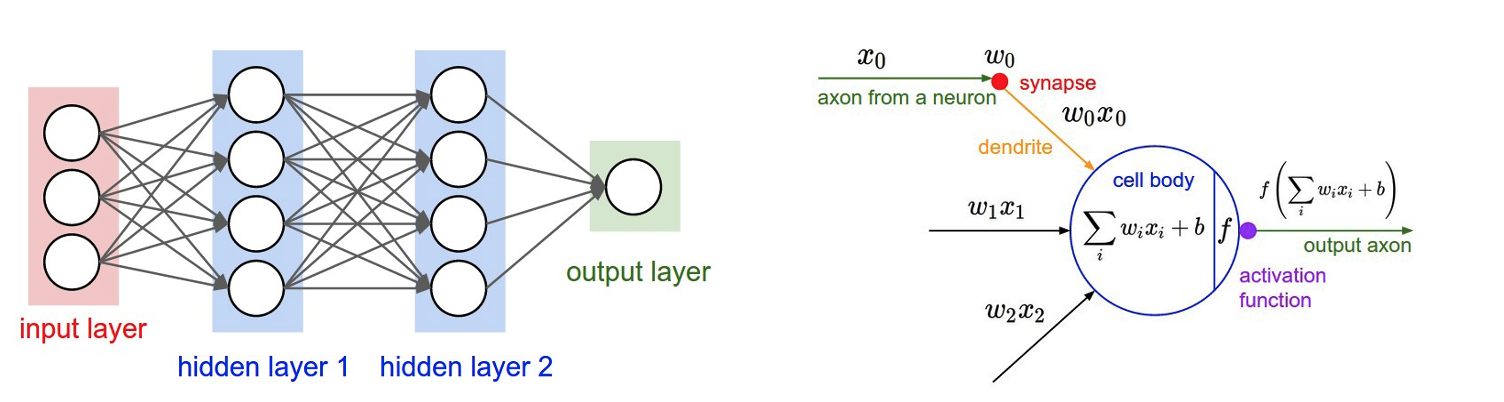
Figure 1. Architecture of a neural network (left) and a single node (right).
The Fnn needs a feature vector to train the network on. As we see from Figure 1, the size of the first layer is the same size as our input feature vector. We convert small molecules to a feature vector by leveraging cheminformatics-based fingerprints (Molecule OE Fingerprint). You can specify the type (p1), bit length (p2), maximum radius (p3), and minimum radius (p4) of these fingerprints in the Cheminformatics Fingerprints parameter. Thus, v1 may be circular, tree, or path; v2 may be 2048, 4096; and so on. When choosing p2, you should be mindful of the relation between the feature vector and the size of the input dataset. One such empirical relation was stated by Hua and coworkers [Hua-2005].
For uncorrelated features, the optimal feature size is N−1 (where N is the sample size).
As feature correlation increases, the optimal feature size becomes proportional to √N for highly correlated features.
This is Optimization Strategy I, which sets the bit length in accordance to the training size.
We can also choose our cheminformatics features based on the nature of the physical property we are trying to predict. For instance, as solubility is more of a local fragment property, keeping the minimum and maximum radii of the fingerprint on the lower end would yield better results. In contrast, properties where different fragments of the molecule interact more may benefit from larger radius sizes. This is Optimization Strategy II.
Besides the cheminformatics features, we may also tweak the machine learning hyperparameters available as the Neural Network Hyperparameter Options.
Note that the parameters take in a list of values and models that will be trained for every possible combination with the other parameters as stated above. Among these parameters, the Sets of Hidden Layers are of particular interest as they dictate the number of nodes in each layer of the network.
These hidden nodes allow the network to learn and exhibit nonlinear behavior.
Thus, if the total number of nodes is too low, it might be insufficient for the network to learn the prediction function. However, a large number of hidden nodes makes the network learn the training set very minutely, thereby losing its ability to generalize. In this case, it would perform poorly for unseen samples. This conundrum of too small versus too large for the size of the hidden layer is known as the underfitting and overfittting problem. A simple rule of thumb to determine this is Optimization Strategy III.
Nh = Ns/(a*(Ni+No))
Ni = number of input neurons. (Equals bit length p2)
No = number of output neurons. (1 for regression networks, >=2 for classification networks)
Ns = number of samples in training data set.
a = an arbitrary scaling factor usually 2-10.
In addition, parameters such as dropouts and regularisers help with overfitting as well. You can train on a set of dropouts and can set a value for L2 regularizers in the Neural Network Hyperparameter Training Option.
Dropouts act by randomly turning off a certain percentage of the node while training. This introduces nondeterministic properties in the model, thereby generalizing it for unseen data.
Regularizers are a great way to prevent overfitting, that is, where the model learns too many details on the training set and is unable to predict for unseen molecules. While there are many techniques to regularize, we choose R2 regularizers since they are smoother and converge easily. Here is an example of a training history of a model which suggests divergence. Adding a regulizer would certainly improve the ability of the model to generalize.
Figure 2. An example of a model whose training history suggests divergence.
Once a model is trained, we can look into the training graphs in the Floe Report (model Link) to gather more insight into the quality of the model built. The graphs illustrate how the mean absolute error (MAE) and mean squared error (MSE) change with every epoch of training. Figure 3 tells us that the learning rate is too high, leading to large fluctuations in every epoch.
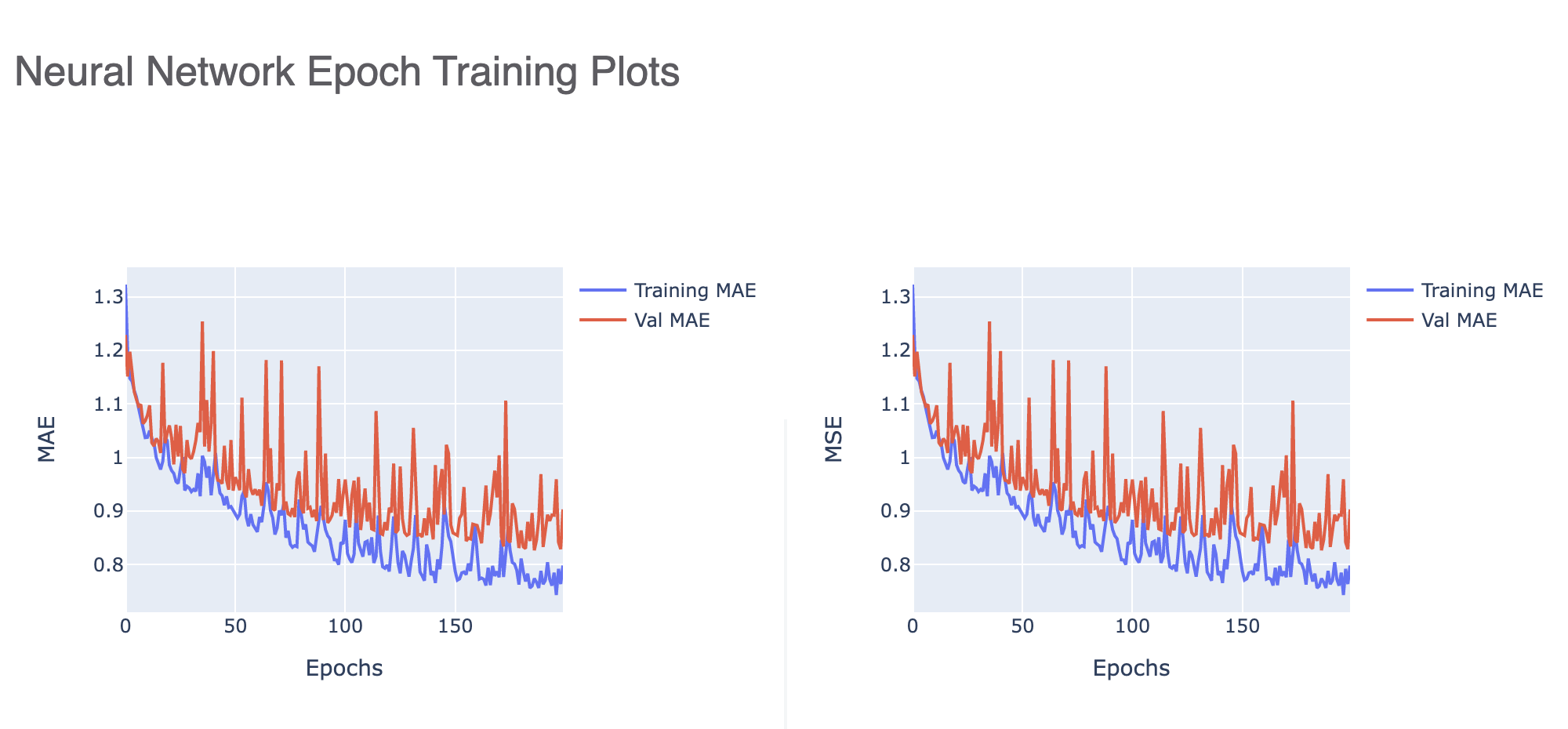
Figure 3. Neural network epoch training plots with a high learning rate.
Figure 4 shows that the validation error is much higher than the training, meaning we have overfit our model. Increasing the regularization parameter or decreasing the number of nodes might be a good way to stop overfitting (Optimization Strategy IV).
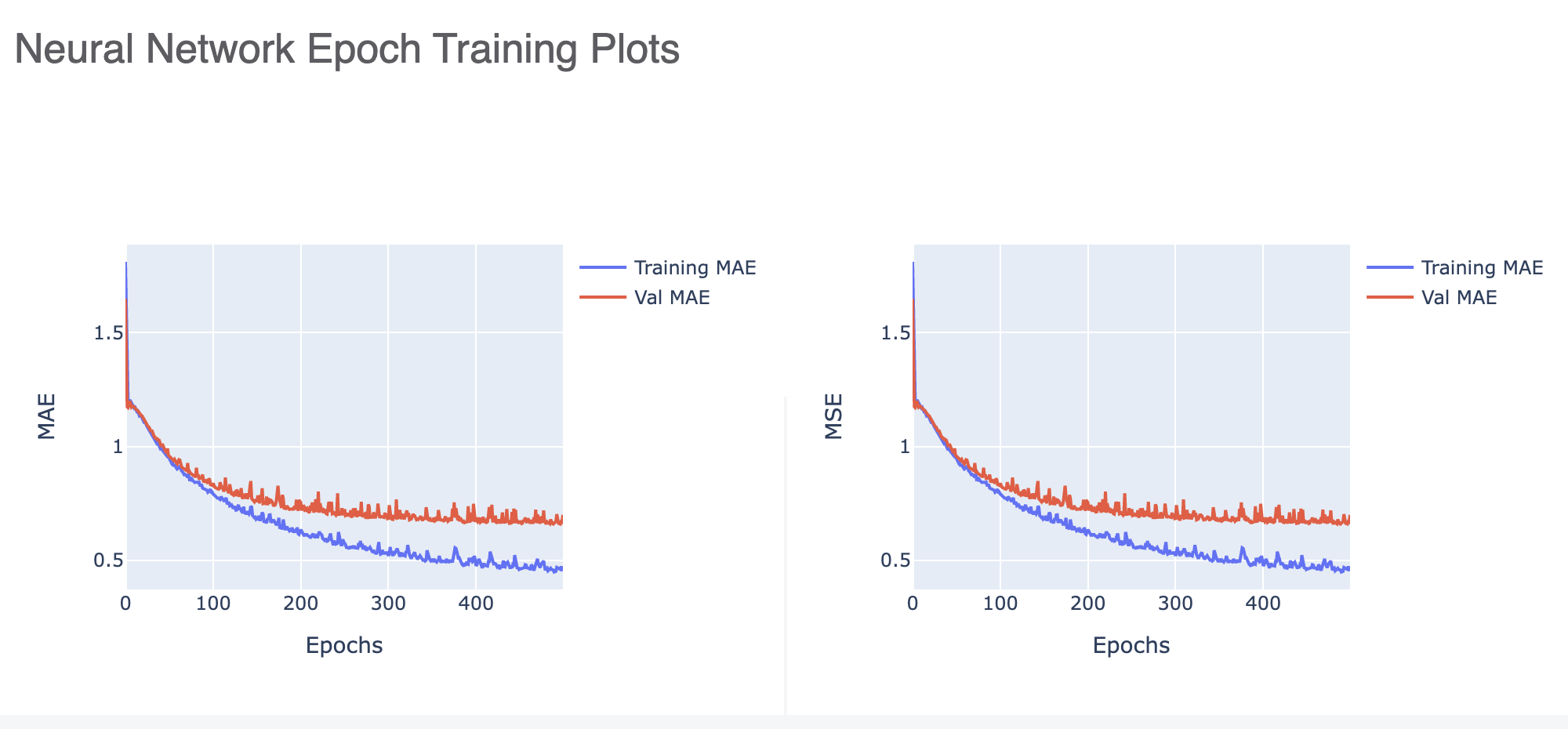
Figure 4. A neural network epoch training plot showing overfitting.
Finally, Figure 5 shows us how a well-trained model should look.
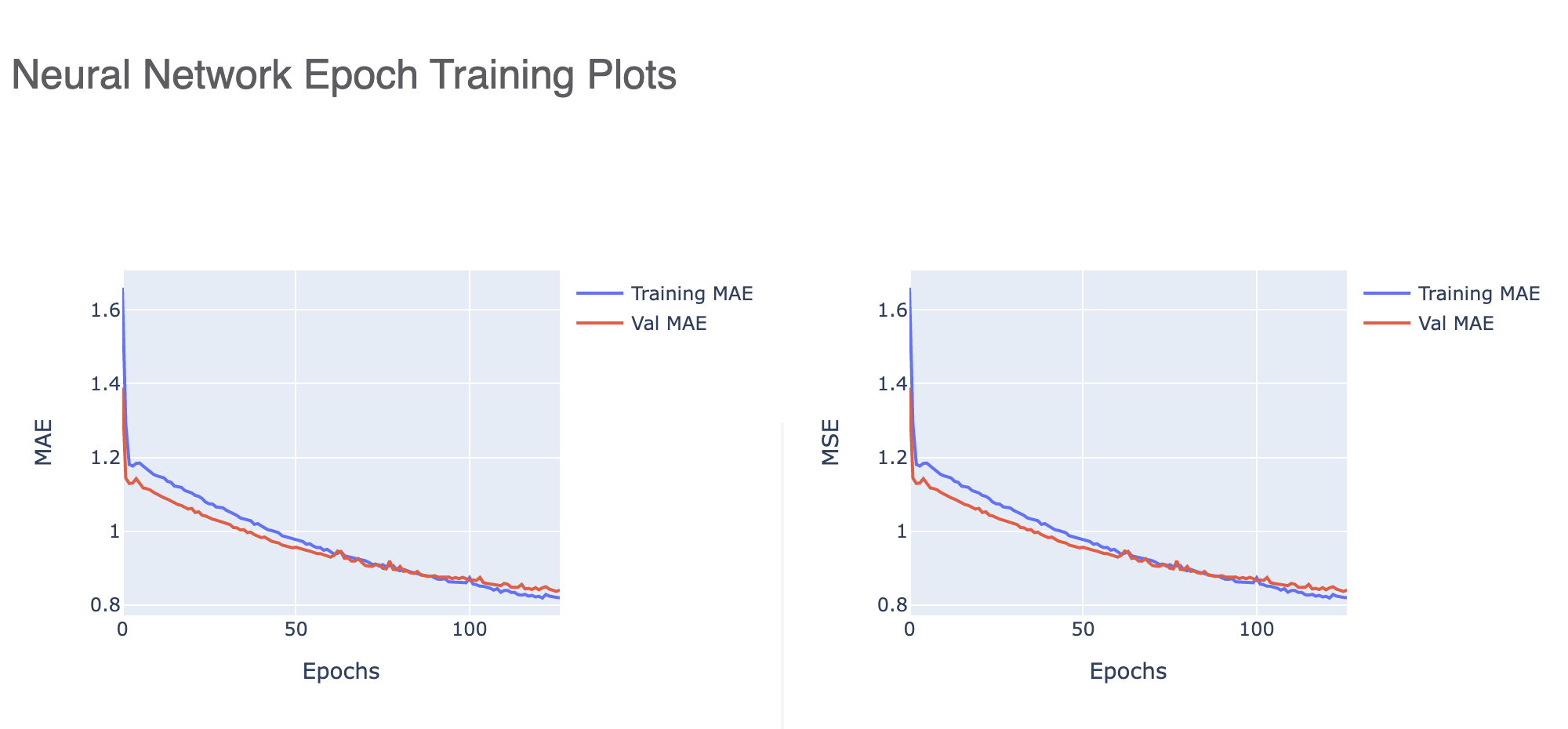
Figure 5. Neural network epoch training plots for a well-trained model.
Library Details of the Floe
Fnn built on Tensorflow Package.
Molecule explanation built on Lime.
Domain of application Tensorflow Probability.